알고리즘 4

DFS(Depth - First Search)와 BFS(Breadth - First Search)

그래프 탐색

DFS: Stack으로 구현, 깊이 우선 탐색

BFS: Queue로 구현, 넓이 우선 탐색

 

그래프를 matrix로 표현하기

package algorism.ch04;

public class UndirectedGraph {

	private int count;
	private int[][] vertexMatrix;
	
//	몇개 짜리 그래프인지 생성자로 받는다.
	public UndirectedGraph(int count) {
		this.count = count;
//		count만큼의 2차원 배열을 만든다.
		vertexMatrix = new int[count][count];
	}
	
//	간선의 유무, 간선 정보를 처리하는 함수
	public void addEdges(int from, int to, int weight) {
		vertexMatrix[from][to] = weight;
		vertexMatrix[to][from] = weight;
	}
	
	public int[][] getMatrix() {
		return vertexMatrix;
	}
}

깊이 우선 탐색(DFS)

• 인접한 노드를 우선 탐색하는 방식
• 스택을 활용하여 구현할 수 있음
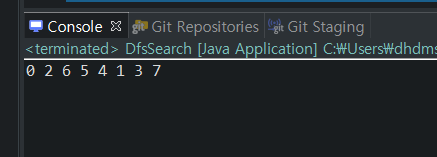
• DFS탐색 순서: 0 - 1 - 3 - 7 - 4 - 5 - 2 or 0 - 2 - 6 - 5 - 4 - 1 - 3 - 7

package algorism.ch04;

import java.util.Stack;

public class DfsSearch {

	int count;
//	방문 유무 변수
	boolean[] visitied;
	Stack<Integer> stack;
	int[][] matrix;
	
	public DfsSearch(int count) {
		this.count = count;
		visitied = new boolean[count];
		stack = new Stack<Integer>();
	}
	
	public void dfsTraversal() {
		
		stack.push(0);
		visitied[0] = true;
		
		while (stack.isEmpty() == false) {
//			꺼냄
			int node = stack.pop();
			System.out.print(node + " ");
			
			for(int j = 0 ; j < count; j++) {
				
				if(matrix[node][j] != 0 && visitied[j] == false) {
//					인접한 요소를 넣어준다.
					stack.push(j);
					visitied[j] = true;
					
				}
			}
		}
	}
	
	public static void main(String[] args) {
		
//		그래프 그리기
		int count = 8;
		UndirectedGraph graph = new UndirectedGraph(count);
		graph.addEdges(0, 1, 1);
		graph.addEdges(0, 2, 1);
		graph.addEdges(1, 3, 1);
		graph.addEdges(1, 4, 1);
		graph.addEdges(2, 5, 1);
		graph.addEdges(2, 6, 1);
		graph.addEdges(4, 5, 1);
		graph.addEdges(3, 7, 1);
		
		DfsSearch dfs = new DfsSearch(count);
		dfs.matrix = graph.getMatrix();
		
		dfs.dfsTraversal();
	}
}

 

너비 우선 탐색(BFS)

• 한 노드에 모든 인접한 노드를 탐색하는 방식
• 큐를 활용하여 구현할 수 있음
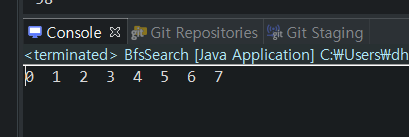
• BFS 탐색 순서: 0 - 1- 2 - 3 - 4 - 5 - 6 - 7

package algorism.ch04;

import java.util.ArrayList;

public class BfsSearch {

	int count;
	boolean[] visited;
	ArrayList<Integer> queue;
	int[][] matrix;
	
	public BfsSearch(int count){
		this.count = count;
		visited = new boolean[count];
		queue = new ArrayList<Integer>();
	}
	
	public void bfsTraversal() {
	
		queue.add(0);
		visited[0] = true;
		
		while(queue.size() != 0) {
			int node = queue.remove(0);
			
			System.out.print(node + "  ");
			
			for(int j = 0; j<count; j++) {
				if(matrix[node][j] != 0 && !visited[j] ) {
					queue.add(j);
					visited[j] = true;
				}
			}
			
		}
	}
	
	public static void main(String[] args) {

		int count = 8;
		UndirectedGraph graph = new UndirectedGraph(count);
		BfsSearch bfsSearch = new BfsSearch(count);
		
		graph.addEdges(0, 1, 1);
		graph.addEdges(0, 2, 1);
		graph.addEdges(1, 3, 1);
		graph.addEdges(1, 4, 1);
		graph.addEdges(2, 5, 1);
		graph.addEdges(2, 6, 1);
		graph.addEdges(4, 5, 1);
		graph.addEdges(3, 7, 1);
		
		bfsSearch.matrix = graph.getMatrix();
		bfsSearch.bfsTraversal();
			
	}
}

 

참고 사이트

https://mygumi.tistory.com/102

[그래프] DFS와 BFS 구현하기 :: 마이구미